C로 미분방정식을 풀어보았다

이 페이지에서 설명하는 프로젝트 코드는 이 저장소에서 찾아볼 수 있다.

세상에나 C보다 Fortran이 더 편해!

학교에서 들었던 수치해석 관련 수업은 총 3개였다. 놀랍게도 그 세 수업 모두 Fortran을 가르쳤다. 그 세 개의 수업 중 2개는 같은 교수가 가르쳤으니까 그렇다고 치지만, 나머지 하나의 수업에서도 Fortran을 배웠다는 건 참 인연이긴 인연이다.

왜 그런 구닥다리 언어가 학교에서는 살아 숨쉬는 지 당시에는 도저히 이해할 수가 없었다. 사실 Fortran이 빠르기는 빠르다. 똑같이 삼체 문제(천체 3개의 궤도를 계산하는 문제. 2개까지는 궤도가 예쁘게 나오는데, 3개 이상부터는 미친년널뛰기를 한다)를 풀었을 때 MATLAB에서는 엄청 버벅거렸는데, Fortran으로 계산하니 행성 한 20개 쯤 더 넣고 시뮬레이션해도 더 빨랐다. 사실 이건 MATLAB이 느려서 생기는 문제가 맞기는 한데… C와 Fortran의 비교는 다음 기회에 해보면 재밌을 듯 하다.

회사 일이 좀 널럴해지니 학교 다니던 때가 벌써 그리워져서인지, 30명 정원에 7명 등록 실제 수강 인원 4명인 수업에서 교수와 함께 오손도손 재밌게 풀던 편미분방정식이 생각나서 갑자기 구현할 삘이 왔다. 대신에 이번에는 연습할 겸 기본 라이브러리만 써서 C로 짜기로 했다. 편집기는 vi를 쓰려고 했지만 역시 Xcode가 100만 배는 더 편한 건 어쩔 수가 없다.

Swift나 Objective-C, Java같은 고급 언어의 세계에 살다 보니 C의 배열은 너무 귀찮다. 정렬 같은 건 기대도 안 하지만, 그래도 최소한 배열의 길이 정도는 알려주면 참 좋을텐데 그딴 게 될 리가 있나. 아쉬운 마음에 내가 직접 선언하도록 한다.

typedef struct _vec {
    unsigned int length;
    unsigned int isAlloc;
    double* arr;
} vec;

어차피 자바처럼 생성자를 만들 수는 없지만 팩토리 패턴 비스무리하게 흉내는 낼 수 있겠다. CGPoint의 CGPointMake(x,y)처럼 팩토리 함수 하나 만들자.

vec vecMake(unsigned int length, double* arr) {
    vec v;
    v.length = length;
    v.isAlloc = 0;
    v.arr = arr;
    return v;
}

vec vecAlloc(unsigned int length) {
    vec v;
    v.length = length;
    v.isAlloc = 1;
    v.arr = (double*)malloc(sizeof(double) * length);
    return v;
}

일부러 버전을 두 가지로 해두었는데, 하나는 벡터(어차피 수치해석에서 1차원 배열은 벡터로 쓸 예정이다)의 값을 알고 있을 때를 위함이고, 하나는 벡터의 값을 전혀 알지 못 하고 그냥 초기화할 때를 위함이다.

생성자를 만들었으니 소멸자도 있어야 수미상관이다. 내친 김에 소멸을 위한 녀석도 만들자. 단, vecMake(int, double*)로 생성한 벡터의 메모리 반환은 알아서 하는 게 맞을 듯 하다.

void freeVec(vec* v) {
    if(v->isAlloc == 1) {
        free(v->arr);
    }
}

바로 이 다음에 나올 코드에서 Fortran의 진가가 발휘된다. C는 배열 간의 사칙연산이 없다. 즉, 이런 게 안 된다.

int arr1[3] = {1, 2, 3};
int arr2[3] = {4, 5, 6};
int arr3[3] = arr1 + arr2 // 말이 될 리가...

사실 C와 그 직계 및 방계 언어로 개발하는 대부분의 개발자에게 이건 상식이다. 그런데 Fortran에서는 이게 된다.

REAL*8, DIMENSION(1:3):: A, B, C
A(1) = 1.0; A(2) = 2.0; A(3) = 3.0;
B(1) = 4.0; B(2) = 5.0; B(3) = 6.0;
C = A + B

그 외에도 굉장히 자잘자잘하게 많다. C에서는 배열 간의 사칙연산도 안 돼, 상수배도 안 돼, 내적 계산도 내가 구현해줘야 해, 함수에서 배열 반환하려면 동적 할당 해줘야 해, 그거 해제 안 하기만 해봐, 하여튼 수치해석용으로 뭔가를 하기에는 매우 귀찮다는 것을 깨달았다.

그 교수님이 Fortran을 사랑한 데에는 사실 다 이유가 있었던 것이다. 솔직히 말해서 자기가 배운 게 Fortran이라 그런 것도 있겠지만, 수업 때 배우는 알고리즘들을 전부 C로 짠다면 생산성이 몇 배로 폭락할 거라는 말은 결국 맞는 말이었던 것이다. 간단한 벡터 연산조차도 개발자가 직접 구현해줘야 하니 이래서야 C를 수업 때 가르치는 건 가성비가 떨어지는 것이다.

사실 이건 C와 Fortran의 목적 자체가 다르기 때문이기도 하다. Fortran은 ‘과학 계산용 언어’라, 거기에 맞는 기능들을 언어 차원에서 제공해줄 뿐이다. 반면 C는 그보다는 더 넓은 목적을 위해 쓰이는 언어이니 Fortran의 각종 편리한 기능들은 애초에 고려 대상조차 아니었을 것이다. 그래도 C는 C인지라 어쨌건 구현하려고 하면 다 할 수는 있다. 이것저것 구현해줘야 할 것들이 좀 잡다해서 그렇지, ODE 정도는 무리없이 구현이 된다는 것을 확인했다.

벡터의 사칙연산을 정의해봅시다

어쨌건 C로 벡터 연산을 흉내내려면 일일이 직접 구현해줘야 한다. 그렇게 어려운 건 아니니 한 번 마무리지어보자.

void vadd(vec a, vec b, vec* output) {
    assert(a.length == b.length);
    output->length = a.length;
    for (int i = 0; i < a.length; i++) {
        output->arr[i] = a.arr[i] + b.arr[i];
    }
}

좀 특이한 점이 있다면, 이 함수는 벡터의 합을 바로 반환하는 것이 아니라 반환을 위한 인자를 따로 받는다는 것이다. 사실 Apple의 Core Graphics를 보면 CGPoint나 CGVector 같은 애들은 벡터 연산 후 값을 바로 반환해준다. 이건 앞의 구조체들 같은 경우에는 벡터의 길이가 고정이기 때문에 가능하다. 난 일부러 임의의 길이의 벡터에도 대응할 수 있도록 벡터의 길이에 제한을 두지 않았기 때문에, 이게 좀 곤란하다. 그래서 어쩔 수 없이 포인터로 결과 값을 받도록 해주었다. 덧셈을 구현했으니 뺄셈, 나눗셈, 곱셈도 마찬가지 방식으로 구현해줄 수 있다.

일반적인 상황을 고려하기

사실 수치해석 과제를 하다 보면 문제 하나만 풀기 위해 코드를 쓰는 경우가 잦다. 그러다 보니 코드의 재활용성은 하늘나라로 간다(그래서 LAPACK 같은 패키지들이 얼마나 잘 짜여져 있는지 알게 된다). 이번에는 그러고 싶지 않았다. 적어도 상미분방정식은 방정식과 초기값만 주어진다면 하나의 코드로 전부 풀릴 수 있게 하고 싶었다. 이러한 목적을 달성하기 위해서는 상미분방정식의 구조를 좀 살펴볼 필요가 있다. 일반적으로 상미분방정식은 다음으로 구성되어 있다.

방정식(Equation)
초기값(Initial value)
제약 조건(Restriction)

방정식

하나하나 구현 방법을 생각해보자. 먼저, 방정식은 함수로 구현하면 될 것이다. 적절한 Input에 적절한 Output이 있으면 되니까. 간단하게 $y' = 2y + t$ 부터 생각해보자. (상)미분방정식은 함수를 찾고자 하기 위한 방정식이고, 미분된 함수는 자기 자신으로 표현된다. 그러니까, 위 방정식은 일반화하면 $y' = f(t, y)$ 인 것이다. 이걸 C로 구현하면 다음과 같이 할 수 있을 것이다.

double test1(double t, double y) {
    return 2.0*y + t;
}

만일 저 방정식 뿐만 아니라 다른 1계미분방정식을 풀고 싶다면, 함수를 다르게 정의하면 될 것이다.

double test2(double t, double y) {
    return -2.0*y*y + sqrt(t);
}

만들다보니 방정식이 선형인지 아닌지도 중요하지 않다. 그냥 함수만 쓰면 된다. 그러므로 구현 목표는 다음과 같다: 모듈에 ‘함수’만 넘겨주고 싶다! 이걸 C로 구현하는 간단한 방법이 바로 함수 포인터를 쓰는 것이다. 그러므로, 함수형을 잘 정의해주는 게 중요하다.

이제 2계 미분방정식도 한 번 풀어보자. 간단하게 $y'' = -y$ 을 생각해보자(이거 풀면 $y(t) = C_1 cos(t) + C_2 sin(t)$ 가 나온다). 쉽게 생각할 수 있는 방법은 다음과 같다.

double test3(double t, double y0, double y1) {
    return -y0;
}

이러면 내가 세운 목표에 모순되는 일이 생긴다: 방정식마다 모듈을 다 새로 만들어줘야 한다. 이건 내가 바라는 상황이 아니다. 정확하게는, 인자의 갯수마다 함수를 새로 만들어줘야 한다. 이걸 해결할 수 있는 방법은 두 가지이다.

가변인자를 받는 함수를 구현한다.
다른 방법을 생각해본다.

가변인자는 나쁜 방법이 아니다. 하지만 만약에 연립미분방정식을 풀게 되면 골치아픈 상황이 생긴다. 예를 들어, 다음과 같은 미분방정식이라면? \begin{align} x’(t) &= 2x(t) + y(t) \\ y’(t) &= -x(t) + 2y(t) \\ \end{align}

double* badIdea(double t, double x, double y) {
    double* arr = (double*)malloc(sizeof(double)*2);
    arr[0] = 2*x+y; arr[1] = -x + 2*y;
    return arr;
}

이게 다 C에서 배열 반환이 골치아프기 때문이다. 만약 고정 사이즈의 벡터라면 구조체를 정의해서 반환하는 것도 가능하지만, 나는 그러지 않기로 했다. 결국 이건 좋은 아이디어가 아니라는 거다.

그럼에도 불구하고 하나의 발상을 얻을 수 있는데, 모든 상미분방정식은 벡터로 표현이 가능하다. 위의 $y'' = -y$ 의 예제도 다음과 같이 쓸 수 있다. \begin{align} y’ &= y’ \\ y’’ &= -y \\ \end{align} 만일 $Y = \begin{pmatrix} y \\\ y' \end{pmatrix}$ 로 정의하면, 이 방정식은 $Y' = f(t, Y)$ 의 형태로 쓸 수 있는 것이다. 그러므로 우리는 방정식을 풀어주는 모듈에 인자로 넘겨줄 함수는 다음과 같은 식으로 구성해야 할 것이다.

void prototype(double t, vec input, vec* output);

초기값과 제약조건

방정식의 입력값은 벡터와 시간으로 하면 된다는 것을 알게 되었다. 그러면 초기값을 어떻게 해줘야 할 지는 자동으로 따라오게 된다. 어차피 초기값이라고 하는 것은 시작점에서의 벡터값이 될 것이므로, 모듈에 전달해줄 초기값의 자료형은 다음과 같이 정의하면 될 것이다.

typedef struct _timeHeader {
    double tFrom;
    double tTo;
    unsigned int interval;
} timeHeader;

typedef struct _inputHeader {
    /* Time Range */
    timeHeader time;
    /* Initial Value */
    vec initialValues;
} inputHeader;

간단히 설명하면, 시간 정보를 나타내는 timeHeader는 언제부터 언제까지, 얼마나 등분할 것인지를 나타내는 구조체이고, inputHeader는 시간 정보와 초기값을 들고 있는 구조체이다.

입력을 넣었으니 출력도 정의해줘야 하는데, 출력은 결국 등분된 시간에 대한 미분방정식의 풀이값이 될 것이므로, 2차원 배열이 필요하다. 이걸 앞에서 정의해둔 vec 구조체를 활용하면, vec의 배열로 정의하면 적절할 듯 싶다.

typedef struct _outputHeader {
    unsigned int length;
    vec* results;
} outputHeader;

outputHeader outputHeaderAlloc(const inputHeader input) {
    outputHeader header;
    header.length = input.time.interval;
    header.results = (vec*)malloc(sizeof(vec) * header.length);
    for (int i = 0; i < header.length; i++) {
        header.results[i] = vecAlloc(input.initialValues.length);
    }
    return header;
}

구조체 생성 및 소멸을 위한 팩토리 함수들은 적절히 구현해주면 될 것이다.

timeHeader timeHeaderMake(double tFrom, double tTo, unsigned int interval);
inputHeader inputHeaderMake(timeHeader time, vec initialValues);
outputHeader outputHeaderAlloc(const inputHeader input);

void freeInputHeader(inputHeader* header);
void freeOutputHeader(outputHeader* header);

미분방정식 풀기

이제 기초공사를 마무리했으니, 미분방정식을 실제로 풀어보자. 미분방정식의 풀이에 사용할 알고리즘은 4th-Order Runge-Kutta라는 방법이다. 미분방정식을 푸는 알고리즘은 사실 다양하다. 가장 기초적인 방식은 미적분학 시간에 간단하게 배우는 Forward Euler Method이다. 문제는 이 방식은 연산을 2배 늘리면(정확하게는 시간 간격을 2배 촘촘하게 하면) 오차도 딱 1/2배만큼만 줄어들고, 10배 늘리면 1/10배만큼만 줄어드는, 상당히 비효율적인 알고리즘이다(아무래도 미분방정식의 풀이에서 시간보다는 정확도가 더 중요해보이는 듯 하다). 그래서 더 효율적인 알고리즘이 필요한데, 그 때 쓰이는 것이 위의 Runge-Kutta 알고리즘이다. 이 알고리즘은 시간 간격을 2배 촘촘하게 하면 오차가 1/16배로 줄어드는, 그래서 훨씬 더 정밀하고, 같은 시간 내에 더 빠르게 정확한 값을 보여주는 알고리즘이다. 이 알고리즘을 구현하기 위해 먼저 함수형부터 정의해주자.

void solveODE(const inputHeader input, outputHeader* output, void (*func)(double t, vec input, vec* output));

앞에서 정의해두었던 inputHeader, outputHeader, 그리고 함수 포인터가 다 등장했다. outputHeader* output이 포인터로 정의된 것은 C의 함수 인자가 call by value 방식으로 넘아가기 때문이다. 이제 차근차근 구현해보자.

void solveODE(const inputHeader input, outputHeader* output, void (*func)(double t, vec input, vec* output)) {
    // Initialize
    const unsigned int VECLEN = input.initialValues.length;
    
    const double dt = (input.time.tTo - input.time.tFrom) / input.time.interval;

    double tOld;
    
    double oldval[VECLEN];
    double newval[VECLEN];

    vec k1 = vecAlloc(VECLEN);
    vec k2 = vecAlloc(VECLEN);
    vec k3 = vecAlloc(VECLEN);
    vec k4 = vecAlloc(VECLEN);
    
    vec fInput = vecMake(VECLEN, oldval);
    vec fTemp = vecAlloc(VECLEN);
    ...

먼저 함수에서 사용할 지역변수들을 초기화해준다. VECLEN 상수는 앞으로 빈번하게 쓰일 예정이라, 타수를 줄이기 위해 상수로 선언해버렸다. dt 역시 시간 간격을 나타내는 변수로서 빈번하게 쓰일 예정이라 미리 상수로 박아놓았다. Runge-Kutta 알고리즘은 이전 값을 바탕으로 현재 값을 계산하는 방식이라, 예전 값과 현재 값이 계속 바뀐다. 즉 지금의 현재 값은 다음 스텝에서는 예전 값이 된다. 그런데 우리는 벡터를 기반으로 모든 연산을 수행할 예정이라, 저렇게 oldval[], newval[]을 정적 배열로 잡아놓았다. k1, k2, k3, k4는 Runge-Kutta 알고리즘 계산에 나오는 임시 변수들이다. 다음 스텝의 값 계산에 필요한 숫자들인데, 최종 아웃풋이 벡터라 중간 결과물들도 벡터여야 한다. 그래서 위에서 정의 vecAlloc를 갖고 할당했는데, 이 함수는 내부적으로 double 배열을 동적할당한다. 그러므로 함수 연산이 끝난 후에 필히 메모리 해제를 해줘야 한다(사실 한 번만 계산하고 말 이런 프로그램들은 딱히 메모리 해제 같은 거 안 해줘도 되기는 하는데, 그냥 좋은 습관이라 생각하자). 동적할당이 싫다면 정적할당 하는 방법도 있긴 한데, 이러면 코드가 쓸데없이 길어지고, 어차피 요즘 컴퓨터로 이 정도의 동적할당은 일도 아니라서 그냥 해제만 잘 해주면 될 듯 하다. fInput, fTemp라는 변수는 구현하다 보면 등장하겠지만, 임시변수들이다. fInput = vecMake(VECLEN, oldval);로 값을 초기화하는데, vecMake 함수는 정적할당을 염두에 두고 구현한 함수이다. oldval 배열의 포인터로 초기화하기 때문에, oldval 배열의 래퍼(Wrapper)라고 생각하면 될 듯 하다.

이제 변수를 잡아줬으니, 초기값을 잡아주도록 하자.

    ...
    // Save initial data to output
    for(int i = 0; i < VECLEN; i++) {
        output->results[0].arr[i] = input.initialValues.arr[i];
    }
    // New value is set to the initial data at first
    for(int i = 0; i < VECLEN; i++) {
        newval[i] = output->results[0].arr[i];
    }
    ...

그 다음, 함수의 본체를 구현해보자.

    ...
    // Iterate and calculate by Runge-Kutta 4th order method
    for (int i = 1; i < input.time.interval; i++) {
        // Move new values to old values
        for(int j = 0; j < VECLEN; j++) {
            oldval[j] = newval[j];
        }
        
        tOld = input.time.tFrom + (i-1) * dt;
        
        // k1 = f(t, Y)
        func(tOld, fInput, &k1);
        vmulScalar(k1, 0.5 * dt, &fTemp);
        vadd(fInput, fTemp, &fTemp);
        // k2 = f(t + 0.5h, y+0.5h*k1)
        func(tOld + 0.5 * dt, fTemp, &k2);
        vmulScalar(k2, 0.5 * dt, &fTemp);
        vadd(fInput, fTemp, &fTemp);
        // k3 = f(t + 0.5h, y+0.5h*k2)
        func(tOld + 0.5 * dt, fTemp, &k3);
        vmulScalar(k3, 1.0 * dt, &fTemp);
        vadd(fInput, fTemp, &fTemp);
        // k4 = f(t + h, y+h*k3)
        func(tOld + 1.0 * dt, fTemp, &k4);
        
        // Calculate new values
        for(int j = 0; j < VECLEN; j++) {
            newval[j] = oldval[j] + (dt/6.0) * (1.0 * k1.arr[j] + 2.0 * k2.arr[j] + 2.0 * k3.arr[j] + 1.0 * k4.arr[j]);
        }
        
        // Save new values to output
        for(int j = 0; j < VECLEN; j++) {
            output->results[i].arr[j] = newval[j];
        }
    }
    ...

만일 Fortran이었다면 코드가 보다 직관적이었을 것이다. 하지만 C에서는 그게 안 되기 때문에, 저렇게 임시변수의 포인터를 넘겨서 계산하는 삽질이 필요하다. 이제 마무리를 해주도록 하자. 사용한 메모리를 반납하면 함수는 끝이 난다.

    ...
    // Clean up, and release all the memories used
    freeVec(&k1);
    freeVec(&k2);
    freeVec(&k3);
    freeVec(&k4);
    freeVec(&fInput);
    freeVec(&fTemp);
}

돌려보기

이제 미분방정식을 푸는 모듈을 만들었다. 실제로 돌려볼 시간이다. 우선 근의 공식이 존재하는 $y' = 2y$ 부터 풀어보자(해석적으로 풀면 $y(t)=Ce^{2t}$ 이다). 너무 큰 범위에서 풀면 힘들테니, 가볍게 $t \in [0,3]$ 정도까지 해보자.

void test01(double t, vec input, vec* output) {
    output->arr[0] = 2.0 * input.arr[0];
}

int main(int argc, const char * argv[]) {
    timeHeader time = timeHeaderMake(0.0, 3.0, 100000);
    vec initialValues = vecAlloc(1);
    initialValues.arr[0] = 1.0;
    inputHeader input = inputHeaderMake(time, initialValues);
    outputHeader output = outputHeaderAlloc(input);
    
    solveODE(input, &output, test01);
    
    fileReport(input, output, "Test01");
    
    freeInputHeader(&input);
    freeOutputHeader(&output);
    
    return 0;
}

함수 test01은 solveODE 함수에 잘 들어갈 수 있도록 함수의 프로토타입을 준수하여 작성하였다. fileReport라는 함수는 outputHeader를 파일에 쓰기 위한 보조 함수로, 그냥 포맷 맞춰서 텍스트 파일에 쓰는 게 전부이다. 이제 결과를 gnuplot을 이용해 그려보면… 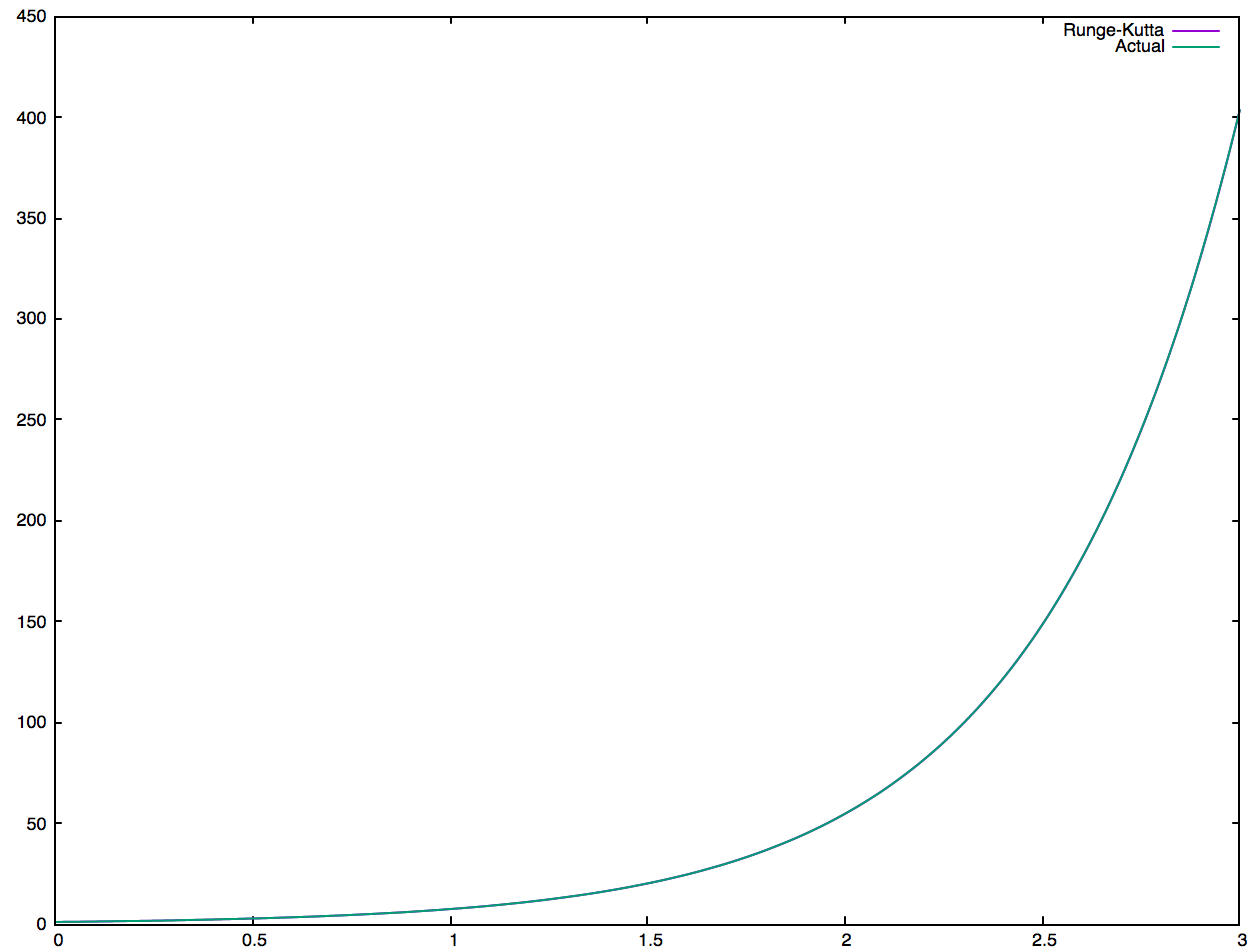Runge-Kutta와 실제 값의 비교 실제와 거의 차이가 없다. 사실 당연한 거긴 한 게, 이 알고리즘은 MATLAB에서도 미분방정식을 풀 때 쓰는 알고리즘이다. 이번에는 그냥 직접 삽질을 해본 것일 뿐이다.

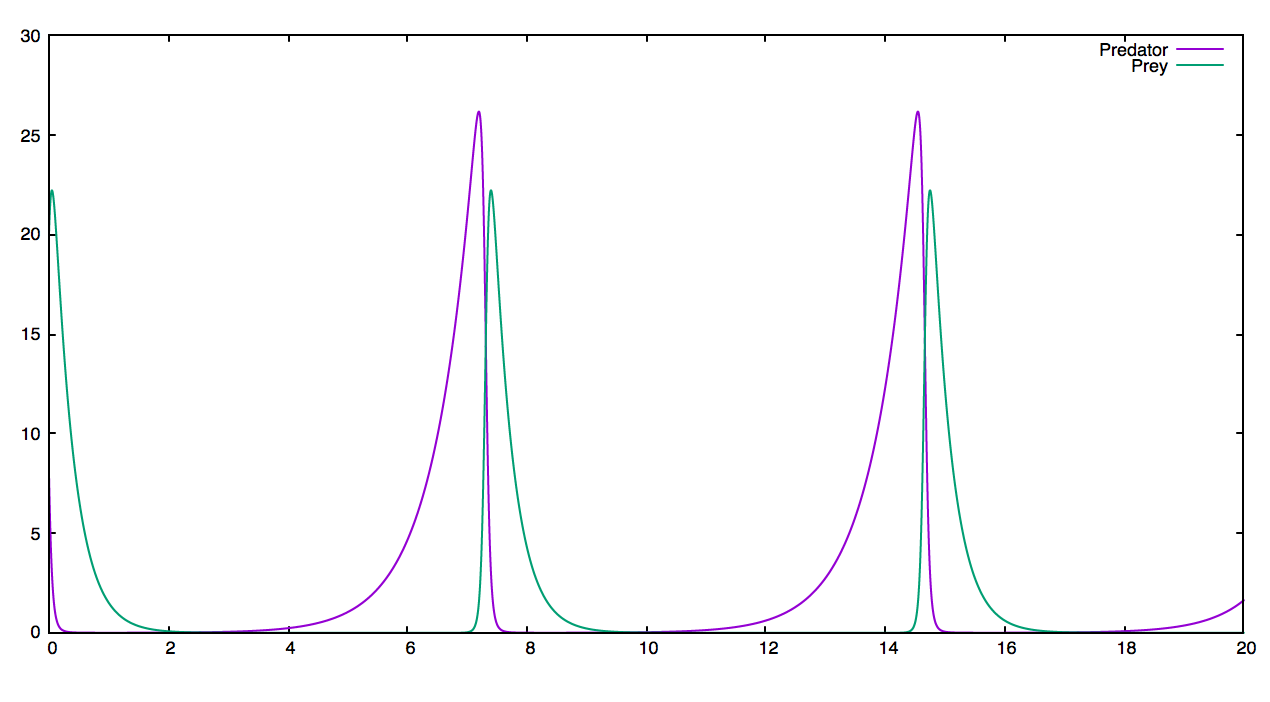
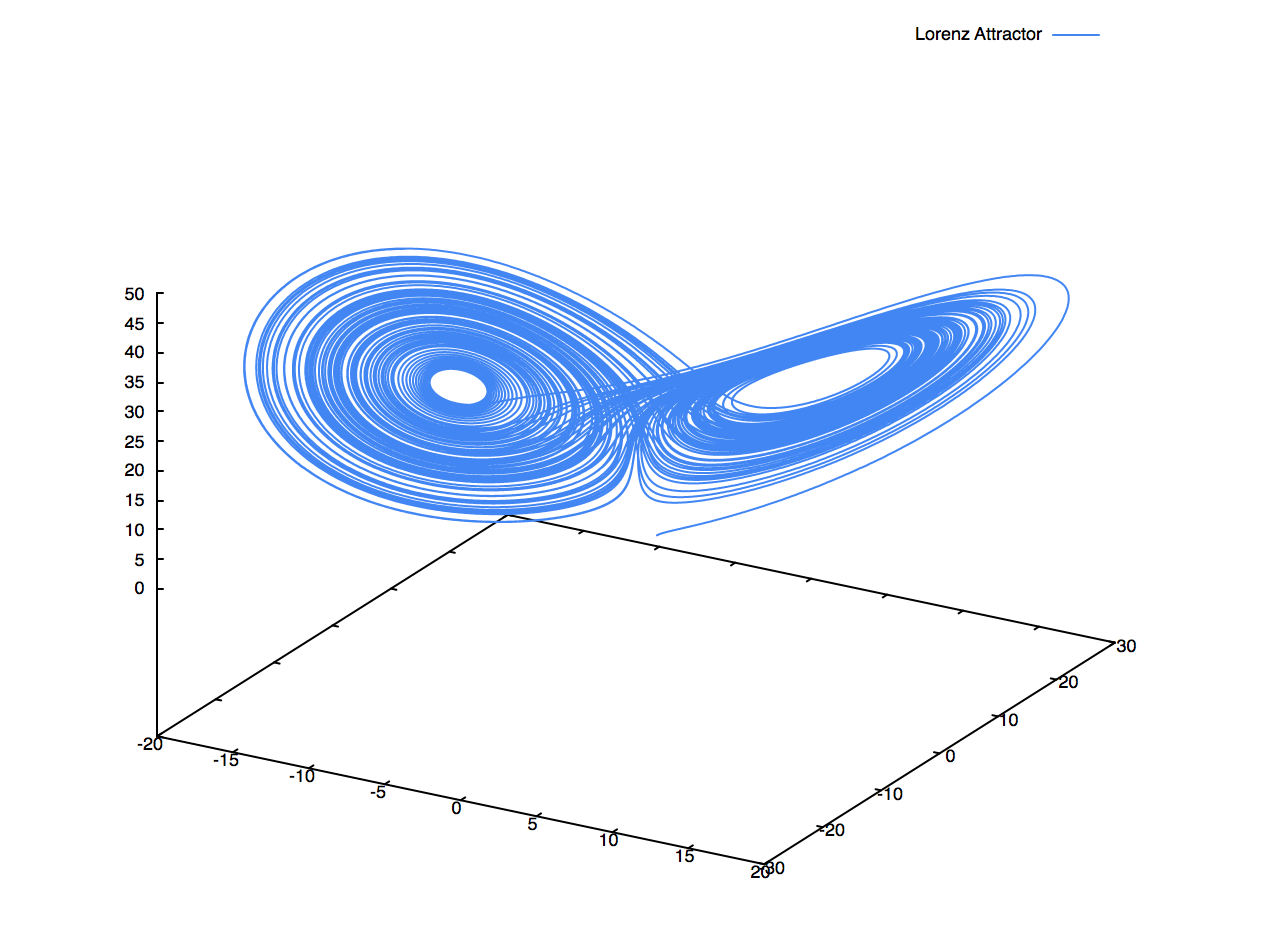
이 모듈을 이용해서 여러 가지 그래프들을 그려볼 수 있는데, Predator-Prey 모델도 그려볼 수 있고, Predator-Prey Model Lorenz Attractor도 그려볼 수 있다.