임의의 분포의 난수 뽑기
이 포스트에서 설명하는 프로젝트의 코드는 이 저장소에서 확인할 수 있다.
Too Long, Didn’t Read
실무에서는 바퀴를 재발명할 필요는 없지만, 취미로서는 한 번쯤은 해볼만한 일인 것 같다. 그래서 이 페이지를 많이 참고하여 Swift로 난수를 만드는 모듈을 만들어보았다.
- 확률변수를 구해보자!
- 적분 계산을 구현한다.
- 스플라인 보간을 구현한다.
- 1과 2를 사용하여 누적확률분포를 만든다.
- 확률변수를 뽑아낸다.

뽑기 구현하기
게임을 하다 보면 뽑기가 자주 등장한다. 왜 나만 황금스킨이 나오지 않는 것일까, 왜 내가 까는 전리품 상자는 다 똥덩어리뿐일까 하는 의구심이 든다면 이건 다 개발자들이 확률을 그렇게 만들어놨기 때문이다. 비단 뽑기뿐만 아니라 많은 현상은 확률분포로 모델링이 가능하다.
사실 프로그래밍으로 뽑기를 구현하는 건 어려운 일은 아니다. 물론 난수 생성 알고리즘을 짜는 건 전혀 다른 문제이지만, 난수 생성 함수가 주어져 있다고 가정하면 뽑기는 그냥 경우의 수로 잘 나눠주는 것 뿐이다.
// 주사위 굴리기
let rand = arc4random_uniform(6)
switch rand {
case 0:
print("1이 나왔어요!")
case 1:
print("2가 나왔어요!")
...
case 5:
print("6이 나왔어요!")
default:
print("이거 버그에요!")
}이제 이 과정을 일반화해보자. 위의 주사위의 눈들처럼 어떤 변수, 또는 사건이 확률적으로 정해지면 확률변수라고 한다(위키페디아에 나와 있는 정의는 읽어봤자 1도 이해 안 된다).
확률변수에서 확률을 계산하는 것은 학교에서 많이 하지만, 정작 확률변수를 만들 일은 잘 없다. 확률변수를 만드려면 먼저 확률분포가 필요하다. 위의 주사위 같은 경우에는 각 눈이 나올 확률이 모두 같기 때문에 쉽지만, 각 눈이 나올 확률이 달라야 한다면 이때부터는 고민이 좀 필요하다.
확률을 계산하는 것은 사건을 갖고 확률을 만드는 함수를 정의하는 것과 같다. 즉, 확률 = f(사건)이다. 여기에서 f(x)의 역할을 하는 녀석이 바로 확률의 분포이다. 그렇다면 사건을 만들어내는 것, 즉 확률변수를 만드는 것은 그 반대의 과정이라고 생각하면 된다. 즉, 사건 = g(확률)인 g를 찾으면 된다.
그러면 저 g라는 녀석이 무엇이냐인데, 수학적으로는 누적확률분포의 역함수이다.
좀 사기같은 주사위를 하나 만들어보자. 주사위의 각 눈이 나올 확률이 자기의 세제곱에 비례한다고 해보자. 그러니까, 2가 나올 확률은 1에 비해 8배, 3은 27배, 6이 나올 확률은 1이 나올 확률의 216배가 되는 초특급 사기 주사위를 만들어보자. 이 주사위가 나올 확률을 그림으로 그려보면 다음과 같다.

초록색 막대는 각 눈의 확률, 주황색 막대는 누적확률분포이다. 만약 컴퓨터에서 난수가 0.5가 나왔다면, 저 그래프에 나오는 것처럼 가로로 선을 하나 그어주고, 가장 먼저 걸리는 주황색 막대를 찾는다. 그 막대가 5번에 세워져 있으므로, 난수 0.5에 대응하는 주사위는 5가 된다.
그러면 분포가 연속이라면?
아 머리아파
연속확률분포가 나오면 머리가 아플 수밖에 없다. 왜냐하면 연속확률분포가 나오면 필연적으로 적분을 해야 하기 때문이다. 확률 자체가 다음과 같이 정의되어 있다. \begin{align} x \in [\alpha, \beta], f(x) \geq 0 \\ \end{align} \begin{align} F(x) = P(X \leq x) = \int_{\alpha}^{x} f(t) dt \\ \end{align}
수식을 보면 머리가 아프다. 하지만 위에서 나온 것과 본질적으로는 똑같은 것이다. 다만 변수가 연속적인 녀석이기 때문에 이에 대응하는 처리가 필요할 뿐인 것이다. 저 수식을 보면 누적확률분포는 다음 식으로 표현이 가능하다는 것을 알 수 있다. \begin{align} u = F(x) = \int_{\alpha}^{x} f(t) dt \\ \end{align} 위에서 사건, 즉 확률분포를 얻으려면 누적확률분포의 역함수가 필요하다고 했었다. 그렇기 때문에 우리에게 필요한 함수는 다음과 같다. \begin{align} x = F^{-1}(u) \\ \end{align} 그런데 적분도 못 하면서 역함수는 어떻게 구해? 라고 생각하면 정상이다. 그렇기 때문에 우리는 꼼수를 써야 한다. 즉, 역함수를 적당히 근사시켜야 한다.
역함수 구하기
예제로 한 번 해보기 위해, 가 우리의 확률밀도함수라고 해보자.
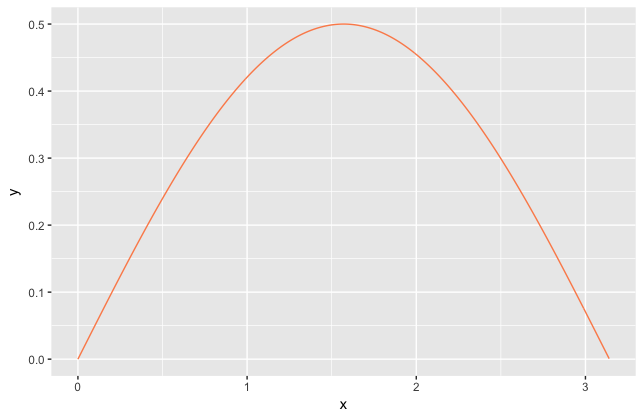
그러면 누적확률분포는 이고, 아래 그림의 초록색 선과 같이 그려진다.
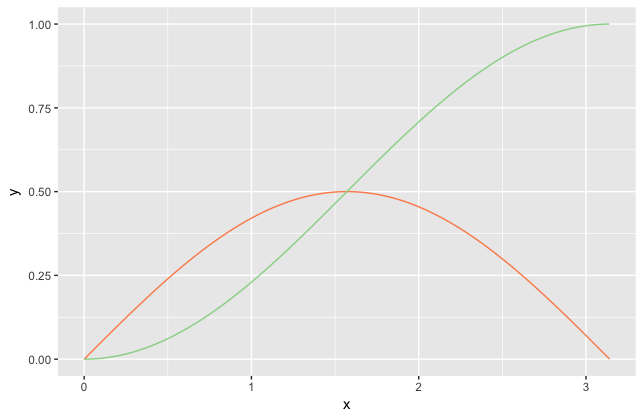
이제 저 초록색 선을 를 기준으로 뒤집자. 그러면 역함수의 모양이 나온다.
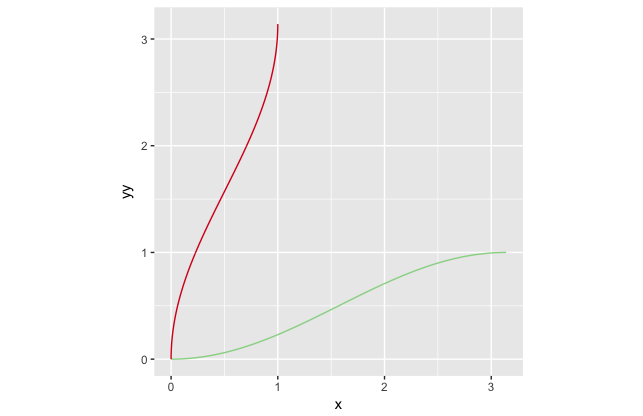
우리는 저 빨간 선이 역함수라는 것도 알고, 저 함수의 식이 라는 것도 구할 수 있다. 문제는 우리의 확률밀도함수가 이렇게 좋은 성질을 가지고 있으리라는 보장은 없다는 것이다.
그렇기 때문에 역함수를 구하기 위해서는 먼저 누적확률분포부터 수치해석적으로 계산해야 한다. 확률밀도함수의 시작을 from이라고 하고, 끝을 to라고 한다면 적당히 구간을 나눈 후에 각 구간별로 직접 다 계산한 표를 갖고 있어야 한다. 수식으로 쓰면 다음과 같다.
\begin{align}
x_i = \alpha + ih, h = \frac{\beta - \alpha}{n} \\
\end{align}
\begin{align}
F_{k} = \int_{\alpha}^{x_k} f(x)dx = \sum_{i=0}^{i=k}\int_{x_i}^{x_{i+1}}f(x)dx \\
\end{align}
즉, 우리는 을 계산해야 한다. 각각의 는 전체 구간보다는 적분 구간이 짧으므로 적분했을 때 오차가 많이 크지 않을 것이다. 이 작은 구간의 넓이를 구하는 방법은 여러가지가 있는데, 나는 Gaussian Quadrature를 구현하였다.
위의 적분을 모두 계산했다면, 우리는 을 얻는다. 수식으로 표현되어서 그렇지, 컴퓨터에서는 Pair의 배열에 불과할 것이다. 이제 이 순서쌍의 와 를 모두 바꿔주면, 그게 바로 역함수가 된다.
역함수를 부드럽게
방금 전에 얻은 역함수는 인데, 이건 이산적인 자료이다. 우리는 역함수 의 에다가 숫자를 집어넣기만 하면 확률변수 가 톽! 하고 튀어나와줬으면 하는데, 만일 인 를 집어넣으면 컴퓨터는 어쩔줄을 모를 것이다. 그렇기 때문에 저 비어있는 곳을 잘 연결해줘야 하는데, 그럴 때 쓰이는 기법이 스플라인 보간법(Spline Interpolation)이다. 사실 주어진 데이터를 부드럽게 잇는 기법에 스플라인 보간법만 있는 건 아니다. 베지에 커브(Beziér Curves)를 사용할 수도 있고, 귀찮으면 그냥 선형보간법으로 땜빵해도 된다. 그러나 여기에서 스플라인 보간법이 사용되는 이유는, 데이터와 데이터 사이를 상당히 부드럽게 이어주기 때문이다. 데이터와 데이터가 부드럽게 연결되어 보인다는 것은 (1)끊어지지 않고 (2)꺾여보이지 않으며 (3)심하게 굽어지지 않아 보인다는 것이다. 이것을 수학으로 해석하면 각각 (1)함수 가 연속이고 (2)함수 이 연속이고 (3)함수 이 연속이라는 것인데, 이것을 만족하는 최소한의 차수의 다항식이 3차함수이다. 결국 스플라인 보간법은 주어진 데이터의 사이사이를 3차함수로 연결하는 알고리즘이다.
스플라인 보간법에 대한 설명은 지나치게 길어지므로 다음 포스트로 넘긴다.
확률변수 계산하기
이제 역함수의 근사치를 얼추 얻어내었다. 그러면 이제 인 에 대해서도 확률변수를 계산할 수 있어야 하는데, 다음과 같은 문제가 있다: 저 가 속하는 구간은 어떻게 찾지?
이 문제는 기초적인 이진 탐색 알고리즘으로 간단하게 해결 가능하다. 일단 가 정렬되어 있다고 가정하면, 이진 탐색 알고리즘을 적용하듯이 가장 가운데 인덱스부터 비교한다. 이 때의 인덱스를 이라고 한다면, 는 다음 세 가지 경우 중 하나이다. \begin{align} &u < F_l \\ F_l &\leq u < F_{l+1} \\ F_{l+1} &< u \\ \end{align} 2번째 케이스라면 우리가 원하는 상황이므로 종료하고, 아닌 경우에는 이진 탐색 알고리즘을 계속 반복하면 된다.
확률변수 그려보기
이제 본격적으로 확률변수를 뽑아보자! 확률변수 생성기는 Swift로 구현하였고, 프로토콜로 두 가지 메소드를 선언하였다.
protocol RandomVariable {
associatedtype T
func generate() -> T
func generate(count: Int) -> [T]
}이산확률변수와 연속확률변수 모두에 대응하도록 구현하였고, 확률변수 생성을 쉽게 하도록 하기 위해 각각 빌더 클래스와 팩토리 클래스도 만들어두었다. 또한 이산확률변수의 경우에는 어떤 오브젝트이건 이에 대응하는 확률을 줄 수만 있다면, 그 오브젝트가 나오도록 하였다. 즉, 제너릭을 사용하여
public class ERDiscrete<T> : RandomVariable {
open func generate() -> T {
...
}
open func generate(count: Int) -> [T] {
...
}
}정의하였기 때문에, 저 T자리에 어떤 클래스나 구조체라도 들어갈 수 있다. 그렇기 때문에 문자열 Foo, Bar가 나올 확률을 각각 42%, 58%라고 줄 수 있다. 일단 코드를 써보고,
let discreteBuilder = ERDiscreteBuilder<String>()
_ = discreteBuilder.append(x: "Foo", p: 0.42).append(x: "Bar", p: 0.58)
let discreteRandoms = discreteBuilder.create().generate(count: 10000)
for foobar in discreteRandoms {
print(foobar)
}돌려보면 그 결과는 다음과 같다.

얼추 비슷하다. 이제 연속확률변수도 한 번 그려보자. 연속확률변수의 경우에는 확률밀도함수, 누적확률함수, 그리고 누적확률함수의 역함수의 세 가지 버전으로 구현하였다. 모두 클로저가 객체 생성에 필요하지만, 실제 구현체는 다르기 때문에 팩토리 클래스를 하나 만들어서 각각 대응하게 하였다. 위에서 정의했던 확률밀도함수인 를 갖고 한 번 실험해보자. 일단 코드를 써보면 다음과 같다.
// Instantiate factory
let continuousFactory = ERContinuousFactory(from: 0.0, to: M_PI)
// Using Probability Density Function
let byPDF = continuousFactory.pdf { sin($0) }.generate(count: 10000)
for x in byPDF {
print("\(x)")
}
// Using Cumulative Density Function
let byCDF = continuousFactory.cdf { 0.5 - 0.5*cos($0) }.generate(count: 10000)
for x in byCDF {
print("\(x)")
}
// Using Inverse Cumulative Density Function
let byICDF = continuousFactory.inverseCDF { acos(1.0 - 2.0 * $0) }.generate(count: 10000)
for x in byICDF {
print("\(x)")
}
// Results should be same

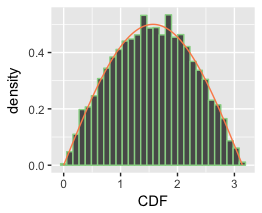

원래의 함수인 와 거의 비슷하다.
참고문헌
How does one generate a random number in Apple’s Swift language?
2WB05 Simulation Lecture 8: Generating random variables