가우시안 수치적분(Gaussian Quadrature)

적분

적분은 주어진 도형의 넓이를 구하는 방법입니다. 물론 수학적인 정의는 더 복잡하지만, 그 시작은 이렇게 단순합니다. 그런데 안타깝게도 적분은 보통은 대단히 어렵습니다. 직사각형의 넓이같이 매우 쉽게 구할 수 있는 도형도 있는 반면, 아예 넓이를 정의할 수 없는 이론상의 도형도 있습니다.

다행히도 현실의 적분 문제는 대부분 근사값을 구하는 것으로 적당히 해결할 수 있습니다. 그리고 그 해결의 근본적 아이디어는 많은 알고리즘에서 사용하는 분할과 정복(Divide and Conquer)입니다. 즉, 복잡한 도형을 여러 개의 작고 단순한 도형으로 쪼갠 다음에, 각각의 넓이를 구해서 합치는 것입니다.

구분구적법

구분구적법은 매우 단순합니다. 도형을 잘 쪼개서 직사각형의 합으로 표현하면 됩니다. 물론, 이 방식으로 하면 오차가 생길 수 밖에 없습니다. 이론적으로는 무한한 횟수로 쪼개게 되면 원래의 도형의 넓이와 같아지겠지만, 현실의 문제에서는 시간도 귀중한 자원이기 때문에, 오차가 적당히 작아지게 되면 그만두게 됩니다.

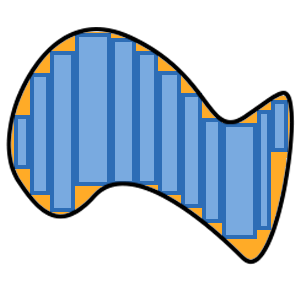
사각형으로 잘게 쪼개면 원래 넓이가 됩니다

리만 적분

리만 적분(Riemann Integration)은 사실 위에서 언급한 구분구적법의 응용입니다. 다만 그 대상이 함수로 바뀌었을 뿐입니다. 사실 함수의 밑넓이도 하나의 도형이기 때문에, 똑같다고 볼 수도 있습니다. 구간을 더 작은 구간들로 나누고, 그 구간에서의 최소값으로 직사각형을 만들고, 최대값으로 직사각형으로 만든 다음에, 합치고 비교하는 과정은 사실 구분구적법과 본질적으로 다르지는 않습니다. 다만 리만 적분은 무한히 쪼갠다는 과정이 들어가기 때문에 더 이론적이랄까요. 최소값으로 만든 직사각형의 합을 무한히 더했을 때의 넓이를 $m$, 최대값으로 만든 직사각형의 합을 무한히 더했을 때의 넓이를 $M$이라고 했을 때, $m = M$이 되었을 때에만 리만 적분으로 넓이를 구할 수 있다고 합니다.

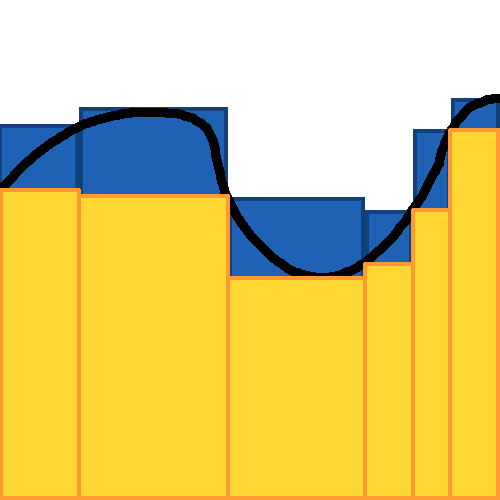
파란색은 구간 내 최대값, 노란색은 구간 내 최소값

여기에서 우리가 고등학교 때 배운 적분의 정의와 뭔가 다르다는 것을 알 수 있습니다. 첫 번째는 나누는 과정입니다. 고등학교에서 배울 때에는 주어진 구간을 균등하게 쪼개야 한다고 배웠는데, 사실 리만 적분은 균등하게 쪼갤 필요가 없습니다. 그냥 막 쪼개도 됩니다. 두 번째는 $m \neq M$인 상황입니다. 고등학교에서는 이런 변태같은 상황은 배우지 않지만, 저렇게 최소값들의 합과 최대값들의 합이 다른 상황이 사실 생기기도 합니다(유리수에서는 1, 무리수에서는 0인 함수가 좋은 예입니다). 다행인 것은, 현실에서는 이것 때문에 고민할 일은 없습니다.

컴퓨터로 구현하기

위의 리만 적분을 이용하면 컴퓨터로 적분 계산을 할 수 있습니다. 이것이 수치 적분(Numerical Integration)으로, 함수의 적분 계산이 필요하기는 한데 손으로 구하기에는 매우 어려운 경우에 활용됩니다.

상황을 간단하게 하여, 위의 리만 적분에서 구간을 균등하게 쪼갠다고 해보겠습니다. 유한한 횟수로 쪼개게 된다면 위의 $m$과 $M$은 거의 대부분 다르게 됩니다. 그렇기 때문에 우리는 적당한 함수의 값을 골라야 하는데, 쪼개진 구간 안에서 가장 왼쪽 값을 고를 수도 있고, 오른쪽 값을 고를 수도 있고, 왼쪽과 오른쪽의 평균값을 고를 수도 있습니다. 특히 평균값을 고르는 경우는 사각형 대신 사다리꼴을 고르는 것과 계산 결과가 같습니다.

조금 더 복잡하게는 그래프를 이차 함수의 연속으로 보고 계산할 수도 있습니다. 이러한 방법을 심프슨의 방법(Simpson’s Method)라고 합니다.

가우시안 수치적분

위의 방법은 뉴턴-코츠 공식(Newton-Cotes Formulas)이라는 방법의 일부입니다. 이 방법의 문제점은 오차를 줄이기 위해서는 구간을 대단히 많이 쪼개야 한다는 것입니다. 즉, 연산량이 늘어납니다. 수치적분 알고리즘은 더 적은 연산으로 더 정확하게를 추구합니다. 그렇다면, 더 나은 방법이 있다면 이를 마다할 이유가 없습니다. 그 방법 중의 하나가 가우시안 수치적분(Gaussian Quadrature)입니다.

가우시안 수치적분은 위의 전략과는 다르게 구간을 균등하게 쪼개지 않습니다. 오히려, 최적의 방식으로 구간을 쪼개는 전략을 취합니다. 그리고 수치적분의 전략 자체도 위의 뉴턴-코츠 방법들과는 약간 다릅니다. 뉴턴-코츠 방법은 넓이의 합이라는 관점인 반면, 가우시안 수치적분은 함수의 합이라는 관점입니다. 사실 ‘함수의 합’이라는 관점이 더 일반적인 관점이기는 한 것 같습니다. 굳이 의의를 붙이자면 ‘넓이의 합’은 기하학적인 관점인 반면 ‘함수의 합’이라는 관점은 대수학적인 관점이랄까요.

가우시안 수치적분은 구간이 $[-1,1]$인 함수 $f(x)$에서 시작합니다. 즉, 목표는 $\int_{-1}^{1}f(x)dx$이지요(이 뜻은, 함수 $f(x)$의 넓이를 $-1$부터 $1$까지 구하겠다는 뜻입니다). 가우시안 수치적분의 목표는 여기에서 시작합니다: $f(x)$가 3차함수라면, 나는 이 넓이는 무조건 정확하게 구하겠다. 즉, $f(x)$를 3차함수로 근사시키겠다는 말과 동일하다고 보면 됩니다. 위에서 언급된 심프슨의 방법이 2차함수였다면, 가우시안 수치적분은 3차함수인 것이지요. 가우시안 수치적분의 결과는 놀랍습니다. 심프슨의 방법이 3개의 점을 필요로 하는 것과 달리 가우시안 수치적분은 2개의 점만 필요합니다. 바로, 다음과 같습니다. \begin{align} \int_{-1}^{1}f(x)dx \approx f(-\sqrt{\frac{1}{3}}) + f(\sqrt{\frac{1}{3}}) \end{align} 어떻게 저런 결과가 튀어나오게 되었는지는 사실 대단히 복잡해서 여기에서는 생략하겠습니다. 하지만 저기에서 나온 $\sqrt{\frac{1}{3}}$은 결코 우연히 튀어나온 결과가 아닌, 대단히 정교한 계산에 의해 나온 숫자입니다.

가우시안 수치적분은 확장성도 대단히 좋습니다. 위에서 든 경우는 3차함수로의 근사였지만, 사실 가우시안 함수는 $n$개의 점을 활용하면 $2n-1$차 함수까지의 정확성을 보장합니다(이 $n$개의 점은 여기를 참고하면 됩니다). 또한 위에서 든 구간은 $[-1,1]$이었지만 구간을 확장하면 임의의 $[a,b]$에 대해서도 계산할 수 있습니다. 게다가 더 응용하면 무한대를 포함한 구간에 대해서도 계산할 수 있습니다.

가우시안 수치적분을 Swift로 구현하면 다음과 같습니다.

class GaussianQuadrature {
    private static let gauss2 = [-0.5773502691896257: 1.0,
                                 0.5773502691896257: 1.0]
    
    private static let gauss3 = [-0.7745966692414834: 0.5555555555555555,
                                 0.0: 0.8888888888888888,
                                 0.7745966692414834: 0.5555555555555555]
    
    private static let gauss4 = [-0.8611363115940526: 0.3478548451374539,
                                 -0.3399810435848563: 0.6521451548625461,
                                 0.3399810435848563: 0.6521451548625461,
                                 0.8611363115940526: 0.3478548451374539]
    
    /*
     * Find definite integral of given function on the given interval
     * Uses Gaussian Quadrature of Order 2, 3, 4
     * Reference: orion.math.iastate.edu/keinert/computation_notes/chapter5.pdf
     */
    
    public static func integrate2(from a: Double, 
                                  to b: Double, 
                                  partition n: Int, 
                                  function f: (Double)->Double)->Double 
    {
        var result = 0.0
        let h = (b-a)/Double(n)
        let cc = h*0.5
        for i in 0..<n {
            let aa = a+h*Double(i)
            for coef in GaussianQuadrature.gauss2 {
                result += coef.value * f(aa + cc * (coef.key + 1.0))
            }
        }
        return cc * result
    }
    
    public static func integrate3(from a: Double, 
                                  to b: Double, 
                                  partition n: Int, 
                                  function f: (Double)->Double)->Double 
    {
        var result = 0.0
        let h = (b-a)/Double(n)
        let cc = h*0.5
        for i in 0..<n {
            let aa = a+h*Double(i)
            for coef in GaussianQuadrature.gauss3 {
                result += coef.value * f(aa + cc * (coef.key + 1.0))
            }
        }
        return cc * result
    }
    
    public static func integrate4(from a: Double, 
                                  to b: Double, 
                                  partition n: Int, 
                                  function f: (Double)->Double)->Double 
    {
        var result = 0.0
        let h = (b-a)/Double(n)
        let cc = h*0.5
        for i in 0..<n {
            let aa = a+h*Double(i)
            for coef in GaussianQuadrature.gauss4 {
                result += coef.value * f(aa + cc * (coef.key + 1.0))
            }
        }
        return cc * result
    }
}

참고문헌

Numerical Quadrature