스플라인 보간법 - 점을 부드럽게 잇기
이 페이지는 이 페이지의 내용을 기반으로 작성되었으며, 구현은 여기를 참고하시면 됩니다. 그리고 수식이 보기 싫으신 분은 맨 밑의 그래프만 보시면 됩니다.
점을 부드럽게 잇기
아래 그림과 같이 흩어진 점들을 어떻게 하면 부드럽게 이을 수 있을까요?

단순히 잇는 것만 생각하면, 그냥 자대고 그으면 됩니다. 하지만 자를 대고 긋게 되면 각 점들에서 심하게 구부러져 보입니다. 즉, 부드럽지 않습니다. 그렇다고 직접 수동으로 부드럽게 잇는 것은 별로 컴퓨터 친화적이지 않습니다. 즉, 알고리즘이 필요합니다.
수학으로 분석하기
어떤 곡선이 ‘부드럽다’는 것의 의미가 무엇인지 생각해봅시다. 우리는 먼저, 곡선이 ‘이어져’ 있어야 부드럽다고 합니다. 즉, 곡선은 연속함수여야 합니다. 그런데 그냥 연속이기만 하면 위에서 본 자대고 그은 선도 부드러워야 합니다. 이건 뭔가 이상합니다. 여기에서 우리는 곡선의 변화도 부드러워야 한다는 것을 알 수 있습니다. 수학적으로 ‘변화’라는 것은 미분으로 해석할 수 있기 때문에, 우리는 어떤 곡선이 부드러우려면 1계 미분도 연속이어야 함을 알 수 있습니다. 더 나아가서, 곡선의 곡률도 부드러웠으면 좋을 것입니다. 곡률이라는 것은 곡선이 굽은 정도인데, 곡선의 각 점마다 굽은 정도가 다 다를 것입니다. 그런데 굽어짐이라는 것도 적당히 부드럽다면, 곡선이 전체적으로 부드러워보일 것입니다. 곡률은 수학적으로 2계 미분, 즉 두 번 미분한 것에 대응하므로, 2계 미분도 연속이어야 함을 알 수 있습니다. 정리하면, 우리가 원하는 부드러운 곡선은 , 즉 2번 미분하여 연속인 함수여야 합니다.
공식 세우기
위에서 세운 원리를 적용하여 공식을 세워보겠습니다. 우리는 보간하는 곡선이 1. 두 번 미분하여 연속이고 2. 계산이 간단 하기를 기대합니다. 2번 조건인 간단한 계산은 다항식이면 충분하므로, 우리는 결국 두 번 미분하여 연속인 다항식으로 보간합니다. 이런 다항식 중 가장 차수가 낮은 다항식은 결국 3차함수입니다. 그래서 이 알고리즘의 이름이 Cubic Spline Interpolation입니다.
먼저, 보간할 점들을 이라고 하겠습니다. 그리고 각 에 대응하는 축 상의 점은 라고 하겠습니다. 즉, 우리는 인 점들을 대상으로 부드럽게 잇습니다.
우리는 을 잇는 공식을 구합니다. 임의의 에 대한 공식을 세우면, 그 뒤로는 에 숫자만 대입하면 되니까요. 먼저, 이후의 편의를 위해 \begin{align} A(x) &:=\frac{x_{k+1}-x}{x_{k+1}-x_{k}} \\ B(x) &:= 1 - A = \frac{x - x_{k}}{x_{k+1}-x_{k}} \\ C(x) &:=\frac{1}{6} (A^3 - A) (x_{k+1}-x_{k})^2 \\ D(x) &:=\frac{1}{6} (B^3 - B) (x_{k+1}-x_{k})^2 \\ \end{align} 로 정의하겠습니다. 그리고 에서의 2계 미분값은 로 쓰겠습니다. 이렇게 쓰면, 우리는 사이에서 보간할 함수는 가 됩니다. 왜 가 저렇게 생겼냐 하면, \begin{align} F_{k}(x_k) &= f_k \\ F_{k}(x_{k+1}) &= f_{k+1} \\ F_{k}^{‘’} (x_k) &= f_{k}^{‘’} \\ F_{k}{‘’} (x_{k+1}) &= f_{k+1}^{‘’} \\ \end{align} 을 만족하는 3차함수는 저거밖에 없기 때문입니다.
이제 를 미분하면 \begin{align} \frac{dF_{k}}{dx} &= \frac{f_{k+1}-f_{k}}{x_{k+1}-x_{k}} \\ &- \frac{3A(x)^2 - 1}{6}(x_{k+1}-x_{k})f_{k}^{‘’} \\ &+ \frac{3B(x)^2 - 1}{6}(x_{k+1}-x_{k})f_{k+1}^{‘’} \\ \frac{d^2 F_{k}}{dx^2} &= A(x)f_{k}^{‘’} + B(x)f_{k+1}^{‘’} \end{align}
특히 , 이므로, 양 끝에서 2계 미분값이 같게 됩니다.
문제는 우리는 저 2계 미분값인 을 모릅니다. 즉, 우리가 방정식을 세워서 구해야 한다는 뜻이 됩니다. 방정식을 세워보기 위해 몇 가지 관찰을 해봅시다. 우리가 구하는 보간된 곡선은 1번 미분해서도 연속이어야 하므로, 에 을 집어넣은 값과 에 을 집어넣은 값이 같아야 합니다. 즉, \begin{align} \frac{dF_{k-1}}{dx} \bigg\rvert_{x_{k}} = \frac{dF_{k}}{dx} \bigg\rvert_{x_{k}} \end{align} 을 만족해야 합니다. 이것이 우리가 풀어야 할 방정식이 되고, 이를 잘 정리하면 \begin{align} \frac{x_{k} - x_{k-1}}{6} f_{k-1}^{‘’} + \frac{x_{k+1} - x_{k-1}}{3} f_{k}^{‘’} + \frac{x_{k+1} - x_{k}}{6} f_{k+1}^{‘’} = \frac{f_{k+1} - f_{k}}{x_{k+1} - x_{k}} - \frac{f_{k} - f_{k-1}}{x_{k} - x_{k-1}} \end{align} 이 됩니다. 그리고 이므로 총 개의 방정식이 나오게 됩니다. 그런데 미지수는 개입니다(). 그렇기 때문에 방정식을 유일하게 풀 수가 없는데, 이 때 몇 가지 조건을 주게 됩니다. 을 조건으로 줄 수 있는데, 이러한 조건 하에서 구하는 보간된 곡선을 Natural Cubic Spline이라고 부릅니다.
풀어보기
우리는 위에서 스플라인 곡선을 구하는 알고리즘을 유도하였습니다. 이 방정식을 조금 간단하게 정리하면 \begin{align} \frac{\Delta x_{k-1}}{6} f_{k-1}^{‘’} + \frac{\Delta x_{k-1} + \Delta x_{k}}{3} f_{k}^{‘’} + \frac{\Delta x_{k}}{6} f_{k+1}^{‘’} = \frac{\Delta f_{k}}{\Delta x_{k}} - \frac{\Delta f_{k-1}}{\Delta x_{k-1}} \end{align}
이 되고, 이걸 더 간략하게 쓰면 다음과 같습니다. \begin{align} X_{k-1} f_{k-1}^{‘’} + Z_{k-1,k} f_{k}^{‘’} + X_{k} f_{k+1}^{‘’} = G_{k-1,k} \end{align}
이걸 행렬로 표현해보면, 다음과 같이 됩니다. \[\left( \begin{array} \delta Z_{0,1} & X_{1} & 0 & … & 0 \\ X_{1} & Z_{1,2} & X_{2} & … & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & … & X_{N-1} & Z_{N-1,N} \\ \end{array}\right) \left( \begin{array} \delta f_{1}^{‘’} \\ f_{2}^{‘’} \\ \vdots \\ f_{N-1}^{‘’} \\ \end{array}\right) = \left( \begin{array} \delta G_{1,2} \\ G_{2,3} \\ \vdots \\ G_{N-1,N} \\ \end{array}\right) \]
이 행렬을 보면 대각 성분과 양 옆밖에 없다는 것을 알 수 있는데, 이렇게 생긴 행렬은 일반적인 경우와 달리 더 빠른 알고리즘으로 풀 수 있습니다. Tridiagonal Matrix Algorithm 또는 Gauss-Seidel Algorithm을 이용하면 의 시간 복잡도로 풀 수 있습니다.
그려보기
위에서 구한 식과 알고리즘을 이용하여 점들을 이어보겠습니다. 이 점들의 좌표는 다음과 같습니다.
7.5 113.5
98.5 172.5
232.5 100.5
367.5 352.5
552.5 296.5
754.5 454.5구현은 Swift로 하였고, 소스 코드는 여기의 spline에서 확인할 수 있습니다.
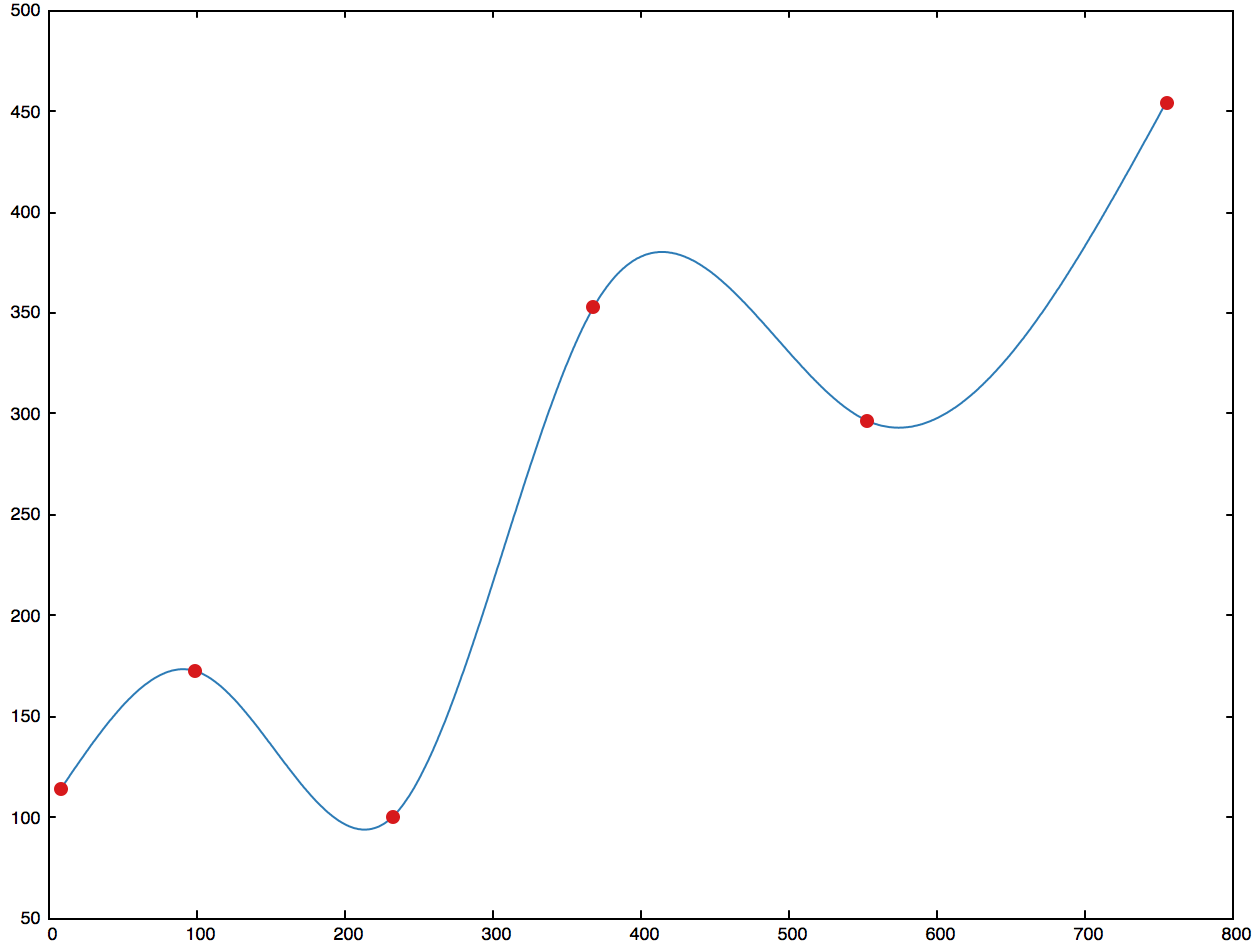
보간한 결과, 자 대고 그은 것보다 훨씬 부드럽습니다.