가챠의 폭력성 (3) - 분석편
이번 편에서는 본격적으로 가챠의 폭력성을 분석해보겠습니다. 분석에 사용된 소스 코드는 이 저장소에서 확인해주세요.
문제가 뭐였더라
문제가 어떤 것이었는지 다시 한 번 보겠습니다.
8개의 아이템을 다 모아야 하는데, 이 아이템은 뽑기 상자(즉, 가챠)를 하나 굴리면 하나가 나온다고 해보자. 이걸 다 모으려면 가챠를 평균 몇 번 돌려야 할까?
좀 더 일반화해보면 다음과 같습니다.
개의 아이템으로 이루어진 집합 이 있다고 하자. 가챠를 한 번 돌리면 의 원소 중 하나가 나오는데, 가 나올 확률을 라고 하자. 그렇다면 가챠를 평균 몇 번 돌리면 집합 의 모든 원소를 다 모을 수 있을까?
그리고 이상적인 가챠를 다음과 같이 정의하겠습니다.
이상적인 가챠는, 모든 아이템이 나올 확률이 동등한 가챠이다.
이상적인 가챠가 있으므로 또라이 같은 가챠도 있습니다. 실험을 위해 최대한 변수를 통제하여 정의하겠습니다.
또라이 같은 가챠는, 한 아이템만 나올 확률이 이고 나머지 아이템은 나올 확률이 동등한 가챠이다.
이론상 평균과 시뮬레이션 결과의 비교
이상적인 가챠로 아이템을 모을 경우, 이론상의 평균은 아래와 같습니다.
\begin{align} M_{n} &= \sum_{k=0}^{n-1} (-1)^{k} \binom{n}{k+1} \left(n-1 + \frac{n}{k+1} \right) \left(1 - \frac{k+1}{n} \right)^{n-1} \\ &= 1 + n \sum_{k=1}^{n-1} \frac{1}{k} \end{align}
실제로 시뮬레이션을 돌려본 결과는 아래와 같습니다. 시뮬레이션은 1부터 30개의 아이템에 대하여, 각각 10000번 씩 수행하였습니다.
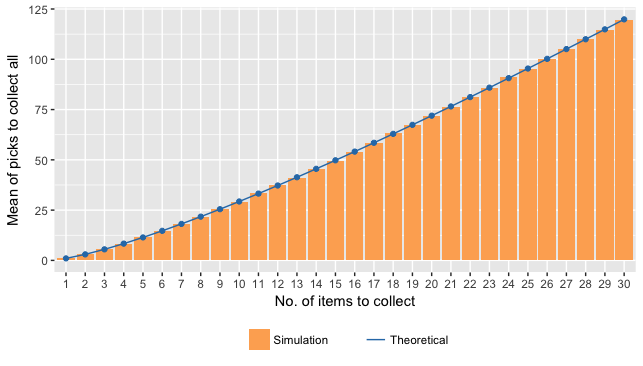
그래프를 보니, 시뮬레이션 결과와 이론상 계산된 결과에 차이는 거의 없습니다. 제가 증명을 잘 한 것 같아 안심이 됩니다.
가챠의 확률분포
하지만 저건 평균입니다. 즉, 운만 좋으면 저는 딱 아이템의 갯수만큼 뽑아서 세트템을 완성할 수도 있고, 재수가 없으면 평생 뽑아도 세트템의 완성 따위 보지 못 할 수도 있습니다. 즉, 될놈될 안될안입니다. 그래서 아이템 갯수가 10개, 20개, 30개일 때 세트템을 완성할 때까지 뽑은 횟수의 히스토그램을 그려보았습니다.
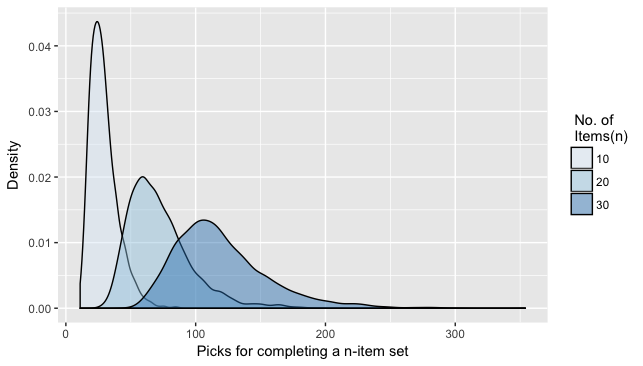
보아하니 오른쪽으로 꼬리가 길쭉한 분포입니다. 10개의 아이템의 경우 평균 30번 정도 가챠를 돌리면 세트템이 완성되는데, 그래프를 보니 운이 없으면 그 이상도 뽑을 수 있습니다. 또 한 가지 특이한 점은, 아이템의 갯수를 늘리면 늘릴수록 히스토그램이 아래로 퍼진다는 것입니다. 그렇기 때문에 아이템의 갯수가 늘면 늘수록, 평균만큼만 뽑아서 세트템을 완성하기는 힘들어집니다.
또라이 같은 가챠의 장난질
이제 가챠를 가지고 장난질을 해보겠습니다. 앞에서 정의한 또라이 가챠를 가지고 테스트를 해보겠습니다. 테스트를 설명하면 다음과 같습니다. 8개의 아이템을 다 모아야 한다고 가정하겠습니다. 그 중 딱 하나만 나올 확률이 매우 작게 하고, 나머지는 나올 확률이 같게 하겠습니다. 예를 들어, 8번 아이템의 경우 나올 확률이 1%이고 나머지 99%의 확률은 7개의 아이템이 사이좋게 나눠가지는 거죠. 이렇게 또라이 같은 정도를 표현하는 숫자를 으로 쓰겠습니다. 테스트는 까지 12개의 급간을 대상으로 수행하였습니다.
일단 히스토그램부터 보겠습니다.
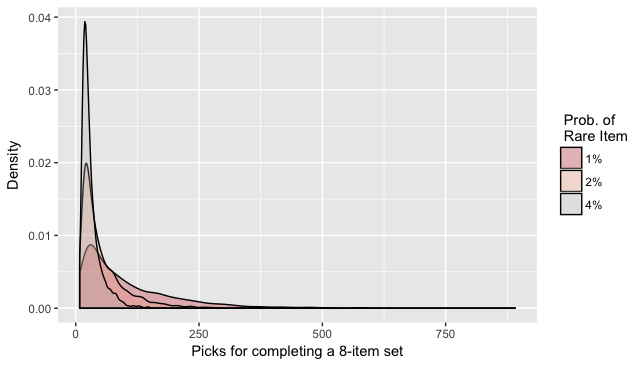
분명히 아이템의 갯수는 8개로 동일한데, 또라이 같은 확률이 작아지면 작아질수록(즉, 뽑기가 어려워지면 어려워질수록) 그래프가 아래로 퍼질러집니다. 네, 뽑기를 어렵게 하는 것과 아이템의 갯수를 늘리는 것은 효과가 같습니다.
이제 평균을 구해보겠습니다. 평균을 구한 그래프는 충격적이었습니다.

주의할 점은 오른쪽으로 갈수록 뽑기가 어려워진다는 것입니다. 뽑기가 어려워지면 어려워질수록 사람들이 평균적으로 돌려야 하는 가챠의 횟수는 지수적으로 커집니다. 극적으로 표현하면, 아이템 하나가 나올 확률이 2%에서 1%로 떨어지면, 가챠를 돌려야 하는 평균 횟수는 거의 2배로 늘어납니다.
결론
이렇게 친구의 떡밥에 낚여서 가챠에 대해 분석해보았습니다. 가챠 무서운 줄은 알았지만 이렇게 무서운 줄은 몰랐습니다. 역시 가챠는 하면 안 되겠습니다.